第 44 场双周赛题解

Q1 1732. 找到最高海拔 (opens new window)

简单模拟，无任何难度

class Solution1732 {
    fun largestAltitude(gain: IntArray): Int {
        var cur = 0
        var ans = 0
        gain.forEach {
            cur += it
            ans = maxOf(ans, cur)
        }
        return ans
    }
}

Q2 1733. 需要教语言的最少人数 (opens new window)

需要注意条件，只可以选择一门语言来教。首先过滤出已经可以交流的好友，他们已经可以不用管了。对于剩下的不可交流的好友，直接看他们会的最多的语言是哪门，那么教这么语言的人就可以最少。

class Solution1733 {
    fun minimumTeachings(n: Int, languages: Array<IntArray>, friendships: Array<IntArray>): Int {
        val study = hashSetOf<Int>()
        friendships.forEach { (a, b) ->
            if (languages[a - 1].all { it !in languages[b - 1] }) {
                study.add(a - 1)
                study.add(b - 1)
            }
        }
        val arr = IntArray(500)
        study.forEach {
            languages[it].forEach {
                arr[it]++
            }
        }
        return study.size - arr.max()!!
    }
}

Q3 1734. 解码异或后的排列 (opens new window)

脑筋急转弯类型的题目。首先注意条件，n是个奇数。举例说明，以5为例，我们给出的数组是

$$\left[ a0 \oplus a1, a1 \oplus a2, a2 \oplus a3, a3 \oplus a4\right]$$

同时，我们知道a0~a5是1到5的组合，因此我们可以知道所有值进行异或后的值，记为result。那么我们把 a1 xor a2的值 和 a3 xor a4的值从result中异或掉，我们就可以得到a0的值，之后直接遍历数组就可以推出原数组了。

class Solution1734 {
    fun decode(encoded: IntArray): IntArray {
        val n = encoded.size + 1
        val ans = IntArray(n)
        ans[0] = 1
        for (i in 2..n) {
            ans[0] = ans[0] xor i
        }
        for (i in 1 until encoded.size step 2) {
            ans[0] = ans[0] xor encoded[i]
        }
        for (i in encoded.indices) {
            ans[i + 1] = encoded[i] xor ans[i]
        }
        return ans
    }
}

Q4 1735. 生成乘积数组的方案数 (opens new window)

数学题目，之前见到过一次类似的，但是比赛时没搞出来。n个数的乘积为k，能够想到需要先将k因式分解。分解成t个质数的乘积，然后将这t个质数分配到n个位置上，由于质数可能是重复的，因此需要使用重复组合的公式。

$$H_{n}^r=C_{n+r-1}^r=\frac{(n+r-1)!}{r!(n-1)!}$$

即，从n个不同元素中，取出r个可重复的元素，有多少种组合。

以(4，12)为例，12可以因式分解为 2 * 2 * 3。一共有4个格子需要填充。对于3的组合，一共有4种，分别可以放在0、1、2、3的格子上，而两个2可以按照刚才的公式(4+2-1)!/2!/3! = 5 * 4 * 3 * 2 / 2 / 3 / 2 = 10，则总组合数为4 * 10。具体示例如下：

质数3的4种组合

质数2的10种组合

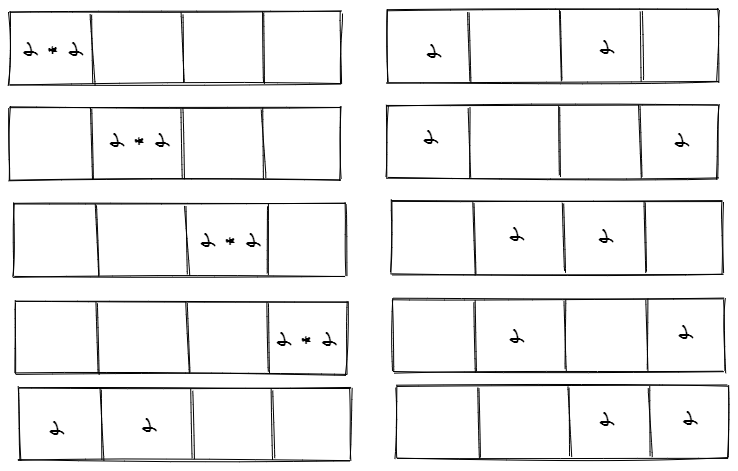
如图所示，3的4种分配与2的10种分配互相独立（乘积不会出现重复结果），因此总分配数可以直接用4*10=40来计算。

下面就可以直接将k的质因数分解出其每个质数所包含的个数即可。同时，由于k的总大小小于10000，我们可以直接枚举出100以内的质数即可。因为大于100的质数至多只能有1个，如果有两个则乘积会大于10000，而将小于100的质数都除完后的k，不为1，则可以认定这个k是个大于100的质数，直接乘以n分配即可（C(n, 1)）。

class Solution5648 {
    fun waysToFillArray(queries: Array<IntArray>): IntArray {
        val mod = 1000000007L
        val primes = intArrayOf(2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97)
        val ans = arrayListOf<Int>()
        queries.forEach {
            var (n, k) = it
            var res = 1L
            for (p in primes) {
                var c = 0L
                if (p > k) break
                while (k % p == 0) {
                    c++
                    k /= p
                }
                res *= longComb(c + n - 1, c)
                res %= mod
            }
            if (k > 1)
                res = res * n % mod
            ans.add(res.toInt())
        }
        return ans.toIntArray()
    }
}

fun comb(m: BigInteger, n: BigInteger): BigInteger {
    var a = BigInteger.ONE
    var b = BigInteger.ONE
    var result = BigInteger.ONE
    val qc = minOf(n, m - n)
    for (j in 0 until qc.toInt()) {
        a = a.multiply(m - BigInteger.valueOf(j.toLong()))
        b = b.multiply(qc - BigInteger.valueOf(j.toLong()))
    }
    result = a / b
    return result
}

fun longComb(m: Long, n: Long): Long {
    return comb(m.toBigInteger(), n.toBigInteger()).mod(BigInteger.valueOf(1000000007L)).toLong()
}