HaKu’s Blog

# 第 225 场周赛题解

# Q1 5661. 替换隐藏数字得到的最晚时间 (opens new window)

题目虽然是Easy，但是代码写起来还是比较复杂，从头开始，每一位为‘?’的Case单独考虑。 看前排大佬们，也有用直接暴力的方案，逆序遍历所有可能性，与当前'?'状态匹配的直接return

class Solution5661 {
    fun maximumTime(time: String): String {
        var (a, b) = time.split(":")
        if (a[0] == '?') {
            a = if (a[1] != '?' && a[1] - '0' > 3)
                "1" + a[1]
            else
                "2" + a[1]
        }
        if (a[1] == '?')
            a = a[0] + "9"
        if (b[0] == '?')
            b = "5" + b[1]
        if (b[1] == '?')
            b = b[0] + "9"
        a = minOf(23.toString(), a)
        b = minOf(59.toString(), b)
        return "$a:$b"
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# Q2 5662. 满足三条件之一需改变的最少字符数 (opens new window)

按照字母来处理，小份字母只能小于等于i，大份字母需要严格大于{i}，大份字母需要严格大于{i}，这之后遍历“a”.."y"的字母即可 这道题很多人都卡在最后两个Case上了（我也WA了两次），主要原因是上述的遍历，如果写成“a”.."z"不合法，因为无法修改字母大于z，故最后的Case会WA

class Solution5662 {
    fun minCharacters(a: String, b: String): Int {
        fun dfs(a: String, b: String): Int {
            var ans = Int.MAX_VALUE
            for (i in 'a'..'y') {
                var diff = 0
                a.forEach {
                    if (it > i) diff++
                }
                b.forEach {
                    if (it <= i) diff++
                }
                ans = minOf(ans, diff)
            }
            return ans
        }
        val n = (a + b).length
        val m = (a + b).groupingBy { it }.eachCount().values.max()!!
        return minOf(dfs(a, b), dfs(b, a), n - m)
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# Q3 5663. 找出第 K 大的异或坐标值 (opens new window)

Q3算是本场比赛中最舒服的题目了，正常DP做即可。因xor的特性，重复计算两次会抵消，所以有

dp[i][j]=dp[i−1][j−1]⨁dp[i][j−1]⨁dp[i−1][j]dp[i][j] = dp[i-1][j-1] \bigoplus dp[i][j-1] \bigoplus dp[i-1][j]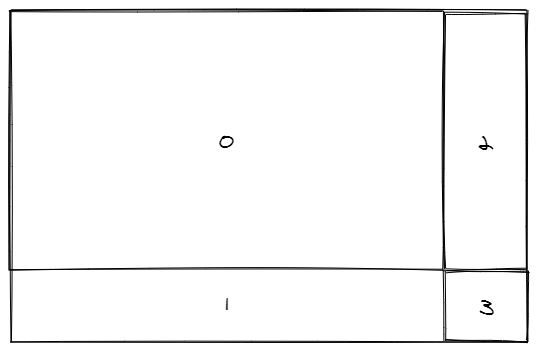

image-20210124132507267

即，对于求3位置来说，左侧异或值 xor 顶部异或值 xor 左上异或值，相当于1、2分别异或一次，而0区域异或3次，根据异或的特性，等价于0、1、2区域分别异或一次，与题意相符

对于求第K个元素，可以用优先级队列（堆实现），只保留K个元素，免去了排序的时间

class Solution5663 {
    fun kthLargestValue(matrix: Array<IntArray>, k: Int): Int {
        val n = matrix.size
        val m: Int = matrix[0].size

        val xor = Array(n) { IntArray(m) }
        val pq = PriorityQueue<Int>()

        for (i in 0 until n) {
            for (j in 0 until m) {
                val a = if (i - 1 >= 0) xor[i - 1][j] else 0
                val b = if (j - 1 >= 0) xor[i][j - 1] else 0
                val c = if (i - 1 >= 0 && j - 1 >= 0) xor[i - 1][j - 1] else 0
                xor[i][j] = matrix[i][j] xor a xor b xor c
                pq.add(xor[i][j])
                if (pq.size > k) {
                    pq.poll()
                }
            }
        }
        return pq.poll()
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# Q4 5664. 放置盒子 (opens new window)

比较讨厌的数学题目。最佳的摆放策略就是沿着墙角摆，然后无法在顶部添加时，才选择增加底部箱子。底部每增加一个箱子，可以增加的总箱子数，有等差数列的规律。

当底部箱子数 总箱子数可达范围 可增加总箱子数
1 1 1
2 2 1
3 3~4 2
4 5 1
5 6~7 2
6 8~10 3
7 11 1
8 12~13 2

根据以上规律，直接循环遍历的增加表格右侧的可增加总数，直到总箱子数可达>=n即可

class Solution5664 {
    fun minimumBoxes(n: Int): Int {
        var bottom = 1
        var sum = 1
        var height = 1
        while (sum < n) {
            var i = 0
            while (i <= height && sum < n) {
                bottom++
                sum += i + 1
                i++
            }
            height++
        }
        return bottom
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

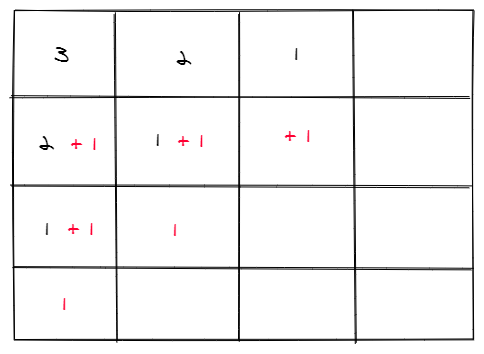
image-20210124134808315

可以根据上图理解，当底部是6的时候，已经达到一个完美状态。此时增加箱子，仅可在底部增加1个。而当再次增加底部箱子时，底部两行可以提供多一个箱子，因此+1底部对总箱子数提供的是+2。而当再次增加一个箱子时，则总数可以+3。最终达到下一次的完美状态。再次从1开始回填。

← 第 224 场周赛 →